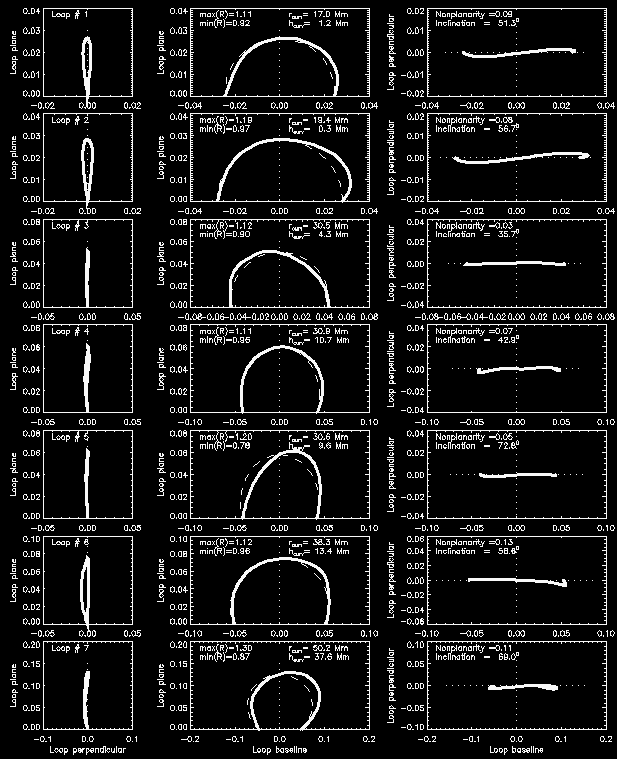
(g2) Orthogonal Projections in the Loop-Plane Coordinate System

Sometimes it is useful to study the projections of the 3D coordinates of loops in a cartesian system that is aligned with the loop plane. If the loops are not coplanar, the loop plane has to be defined by 3 points, for which we choose the first and last spline point of the loop (supposedly the footpoints), which define the baseline direction. The loop plane is defined in addition by a 3rd point, for which we choose the loop apex position above the midpoint of the baseline. We need the 3D coordinates from the loop datafile (LOOPFILE) and the image parameters (PARA) from the savefile (SAVEFILE). Let us assume we have the 3D coordinates of 30 loops in the datafile, but select only the first 7 complete loops (LOOPNR=[1,7]):

IDL>
loopfile ='loop_A.dat' ;output filename where 3D coordinates of loops are stored
savefile='loop_A.sav'
restore,savefile ;restore saved data from step (2a)
loopnr =[1,7] ;range of loop numbers (loop number 1 corresponds to IDL index 0 in loopfile)
euvi_orthogonal,loopfile,loopnr,para

The output on the screen will look like this:




You find also a postscript file with the name ortho.ps